Codeforces Educational Round #2

    CF的第二场“Hacker大赛”，被Hack两发，华丽落榜，unrated。

    题目整体还是简单基础，计算几何又来虐精度刷存在感...水题无爱，计算几何无爱，重点说说E题。

    题意：分离出字符串中的非负整数，非负整数的定义是

0|[1..9][0..9]*

    解法：简单自动机的实现。

    code

    题意：找到序列中小于等于某数的项的个数。

    解法：C++ STL的 upper_bound()，注意upper_bound返回的是一个对应位置的指针，减去数组的指针得到下标。用二分自己实现也很简单。

    code

    题意：给出一些字符，求修改最少的字符使之可以形成回文串，且回文串尽量字典序最小的方案。

    解法：因为都是小写字母，总共也就26个字符。统计所有字母出现个数，从a向z扫，如果某个字母是单数个，就从z向a找出第一个是单数的，后者修改为前者既是最佳方案。因为假如总共有k个字母的个数是奇数个，那么最少修改次数一定是k/2，这是显而易见的。然后把字典序较大的字符修改为尽可能小的也是贪心最优的。这题竟然错到了输出环节，被人Hack了一发，也是醉了...

    code

    题意：两圆交面积。

    解法：中学数学...又是精度？官方Editorial讲的挺好，不提了。

    code

    题意：一棵树，每个节点都有一种颜色。一个节点的“主导色”定义为——这个节点为root的子树中，出现最多的颜色（如有多个，则为其和）。求每个节点的“主导色”。

    解法：

        先说说暴力的做法，复杂度是O(n^2*logn)的。应该一下子就能想到吧：

 void dfs(int x){
	visited[x] = true;
	maxcnt[x] = 1;
	ans[x] = c[x];
	for (vector::iterator it = edges[x].begin();it != edges[x].end();it++){
		if (visited[*it]) continue;
		int y = *it;
		dfs(y);
		int mx = mapnum[x], my = mapnum[y];
		for (map<int,int>::iterator mit = mcnt[my].begin(); mit != mcnt[my].end(); mit++){
			mcnt[mx][mit->first] += mit->second;
			if (mcnt[mx][mit->first] > maxcnt[x]){
				maxcnt[x] = mcnt[mx][mit->first];
				ans[x] = mit->first;
			}
			else if (mcnt[mx][mit->first] == maxcnt[x]) ans[x] += mit->first;
		}
	}
}       
        

        比赛的时候并没有想出来还能怎么优化，但看到题解感觉被亮瞎了。所谓的优化，只是在每次合并的时候遍历小的map，合并到较大的map，复杂度竟然就变成了O(n*logn*logn)。先上代码：

void dfs(int x){
	visited[x] = true;
	maxcnt[x] = 1;
	ans[x] = c[x];
	for (vector::iterator it = edges[x].begin();it != edges[x].end();it++){
		if (visited[*it]) continue;
		int y = *it;
		dfs(y);
//<<<<
		if (mcnt[mapnum[x]].size() < mcnt[mapnum[y]].size())
			swap(mapnum[x],mapnum[y]),ans[x] = ans[y],maxcnt[x] = maxcnt[y];
//>>>>
		int mx = mapnum[x], my = mapnum[y];
		for (map<int,int>::iterator mit = mcnt[my].begin(); mit != mcnt[my].end(); mit++){
			mcnt[mx][mit->first] += mit->second;
			if (mcnt[mx][mit->first] > maxcnt[x]){
				maxcnt[x] = mcnt[mx][mit->first];
				ans[x] = mit->first;
			}
			else if (mcnt[mx][mit->first] == maxcnt[x]) ans[x] += mit->first;
		}
	}
}
        

        首先，实现方法上——思路很巧妙，map并没有固定到某一个节点上，而是节点记录指向某个map的索引，交换map时只需要交换索引即可；但要记得同时将其他状态也进行传递。

        然后，复杂度——每次合并的复杂度由较小map的size决定。考虑根节点1的合并复杂度，假设其孩子的子树含有的节点数分别为a1,a2,a3...ak； 那么根节点1上的总合并复杂度是

O = 1+max(1+a1,a2)+max(1+a1+a2,a3)+...+max(1+a1+a2+...+a(k-1),ak)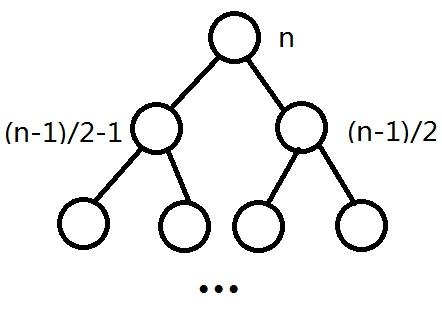

        基本就是一棵完全二叉树了，节点数依次平分，每层的复杂度都是O(n)，共logn层，故全局合并复杂度(指所有的合并遍历的较小map中结点的总数)是O(n*logn)，当然每次合并的时候还是要查较大map的，所以总体复杂度是O(n*logn*logn)。

        不能保证以上说明（非证明）是正确的，但应该能说明一些问题，比官方Editorial解释的更详尽一点吧。数学不过关，算导看不动，感觉上只能解释到这儿了。

        思想很神奇，效果拔群，以后遇到类似的题可以往更深层理解一点。

    code

    题意：

    解法：

    code

Copyright © 2015-2016 zhyack. All Rights Reserved.